题目内容
12.已知函数y=f(x+2)的定义域为(-1,0),则(f|2x-1|)的定义域为(-$\frac{1}{2}$,0)∪(1,$\frac{3}{2}$).分析 由函数y=f(x+2)的定义域,得到x+2的范围,由此求得|2x-1|的范围得答案.
解答 解:∵y=f(x+2)的定义域为(-1,0),即-1<x<0
得1<x+2<2.
∴1<|2x-1|<2,解得:-$\frac{1}{2}$<x<0或1<x<$\frac{3}{2}$,
故答案为:(-$\frac{1}{2}$,0)∪(1,$\frac{3}{2}$).
点评 本题考查了函数的定义域及其求法,关键是掌握该类问题的解决方法,是基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.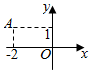 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.已知函数f(x)=log2(2-ax)在(-∞,1]上是减函数,则a的范围是( )
| A. | [1,2] | B. | (1,2) | C. | (1,+∞) | D. | (-∞,2) |