题目内容

10．函数$f（x）={x^2}-\frac{1}{2^x}$的零点有（　　）个．
A．1B．2C．3D．4

分析 函数的零点个数转化为方程的根的个数，转化为两个函数的图象交点个数，画出函数的图象即可判断选项．

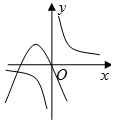
解答 解：函数$f（x）={x^2}-\frac{1}{2^x}$的零点，就是方程x2=$\frac{1}{{2}^{x}}$的根的个数，也就是y=x2与y=$\frac{1}{{2}^{x}}$的交点个数，画出两个函数的图象如图：
两个函数有3个交点．
故选：B．

点评 本题考查数形结合，函数的零点个数的判断，考查转化思想以及计算能力．

练习册系列答案
相关题目
20．已知f（x）=$\left\{\begin{array}{l}{x-5（x≥7）}\\{f（x+3）（x＜7）}\end{array}\right.$（x∈N），那么f（3）等于（　　）
A．2B．3C．4D．5
1．定义在R上的偶函数f（x），在[0，+∞）是增函数，若f（k）＞f（2），则k的取值范围是{k|k＞2或k＜-2}．
18．已知f（x）=logmx（m为常数，m＞0且m≠1），设f（a1），f（a2），…，f（an）（n∈N+）是首项为4，公差为2的等差数列．
（Ⅰ）求证：数列logman=2n+2，{an}是等比数列；
（Ⅱ）若bn=anf（an），记数列{bn}的前n项和为Sn，当m=$\sqrt{2}$时，求Sn．
5．已知数列{an}满足a1+2a2+3a3+…+nan=n+1（n∈N*），则数列{an}的通项公式${a_n}=\left\{{\begin{array}{l}{2（n=1）}\\{\frac{1}{n}（n≥2）}\end{array}}\right.$．
15．已知函数$f（x）={a^{3{x^2}-3}}$，$g（x）={（{\frac{1}{a}}）^{5x+5}}$，其中a＞0，且a≠1．
（1）若0＜a＜1，求满足不等式f（x）＜1的x的取值的集合；
（2）求关于x的不等式f（x）≥g（x）的解的集合．
2．设f（x）是定义在（-1，+∞）内的增函数，且f（xy）=f（x）+f（y）若f（3）=1且f（a）＞f（a-1）+2
求：
（1）f（9）的值，
（2）求a的取值范围．
19．在数列{an}中，前n项和为Sn，且Sn=$\frac{n（n+1）}{2}$，数列{bn}的前n项和为Tn，且bn=$\frac{{a}_{n}}{{2}^{n}}$
（1）求数列{an}的通项公式；
（2）是否存在m，n∈N*，使得Tn=am，若存在，求出所有满足题意的m，n，若不存在，请说明理由．
20．二次函数y=ax2+bx和反比例函数$y=\frac{b}{x}$在同一坐标系中的图象大致是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网