题目内容
小明手中有5张扑克牌，其中2张为不同花色的k，3张为不同花色的A．规定每次只能出同一种点数的牌（可以只出一张，也可出多张），出牌后不再后收回，且同一次所出的牌不考虑顺序，若小明恰好4次把牌出完，则他不同的出牌方式种数共有（ ）
| A、48 | B、74 | C、96 | D、98 |
考点：计数原理的应用
专题：排列组合
分析：根据题意，5张扑克牌恰好4次把牌出完，则必须有一次出2张同一种点数的牌，先确定这两张，当这两张2张为不同花色的k时和当这两张2张为不同花色的A时，分别计算每种情况的出牌方法数目，由分类计数原理计算可得答案．
解答：
解：根据题意，5张扑克牌恰好4次把牌出完，则必须有一次出2张同一种点数的牌，先确定这两张，
分两类，当这两张2张为不同花色的k时，有
=24种，
当这两张2张为不同花色的A时，有
•
=72种，
根据分类计数原理，则他不同的出牌方式种数共有24+72=96种
故选：C
分两类，当这两张2张为不同花色的k时，有
| A | 4 4 |
当这两张2张为不同花色的A时，有
| C | 2 3 |
| A | 4 4 |
根据分类计数原理，则他不同的出牌方式种数共有24+72=96种
故选：C
点评：本题考查排列、组合的应用，解题的关键在于全面考虑，按一定顺序分类讨论、计算，做到不重不漏，属于基础题．
练习册系列答案
小学教材完全解读系列答案
相关题目
“a=1”是“直线l1：ax+y-1=0与直线l2：4x+（a+3）y+5+a=0平行”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
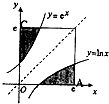如图，在边长为e（e为自然对数的底数）的正方形区域的A处于C处各有一个通信基站，其信号覆盖范围分别为如图所示的阴影区域．该正方形区域内无其它信号来源且这两个基站工作正常，若在该正方形区域内随机选择一个地点，则该地点无信号的概率为（ ）A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
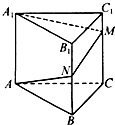已知三棱柱AB-A1B1C1的侧棱垂直于底面，且底面边长与侧棱长都等于3，蚂蚁从A点沿侧面经过棱BB1上的点N和CC1上的点M爬到点A1，如图所示，则当蚂蚁爬过的路程最短时，直线MN与平面ABC所成角的正弦值为关于函数f（x）=x2（lnx-a）+a，给出以下4个结论：
①?a＞0，?x＞0，f（x）≥0；
②?a＞0，?x＞0，f（x）≤0；
③?a＞0，?x＞0，f（x）≥0；
④?a＞0，?x＞0，f（x）≤0．
其中正确结论的个数是（ ）
①?a＞0，?x＞0，f（x）≥0；
②?a＞0，?x＞0，f（x）≤0；
③?a＞0，?x＞0，f（x）≥0；
④?a＞0，?x＞0，f（x）≤0．
其中正确结论的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
已知等差数列{an}的公差为d（d＞0），a1=1，S5=35，则d的值为（ ）
| A、3 | B、-3 | C、2 | D、4 |