题目内容
9.tan2016°的值所在的大致区间为( )| A. | (-1,-$\frac{\sqrt{3}}{3}$) | B. | (-$\frac{\sqrt{3}}{3}$,0) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{3}$,1) |
分析 由条件利用诱导公式、正切函数的单调性,得出结论.
解答 解:∵tan2016°=tan(180°•11+36°)=tan36°,
又∵tan30°=$\frac{\sqrt{3}}{3}$,tan45°=1,36°∈(30°,45°),
函数y=tanx在(0°,90°)上单调递增,
故tan36°∈($\frac{\sqrt{3}}{3}$,1),
故选:D.
点评 本题主要考查诱导公式、正切函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某小型贸易公司为了实现年终10万元利润目标,特制定了一个销售人员年终绩效奖励方案,当销售利润为x万元(4≤x≤10)时,奖金y万元随销售利润x的增加而增加,但奖金总数不超过2万元,同时奖金不超过销售利润的$\frac{1}{2}$,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7)( )
| A. | y=0.4x | B. | y=lgx+1 | C. | y=x${\;}^{\frac{3}{2}}$ | D. | y=1.125x |
4.以(-2,1)为圆心且与直线x+y=3相切的圆的方程为( )
| A. | (x-2)2+(y+1)2=2 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=8 | D. | (x+2)2+(y-1)2=8 |
14.设直线l:y=3x-2与抛物线Γ:y2=4x交于A、B两点,过A、B两点的圆与抛物线Γ交于另外两个不同的点C、D,则直线CD的斜率k=( )
| A. | -$\sqrt{6}$ | B. | -2 | C. | -3 | D. | -$\frac{1}{3}$ |
19.执行如图的程序框图,若输人a=319,b=87,则输出的a是( )


| A. | 19 | B. | 29 | C. | 57 | D. | 76 |
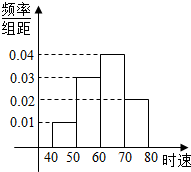 5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:
5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问: