题目内容
14.设直线l:y=3x-2与抛物线Γ:y2=4x交于A、B两点,过A、B两点的圆与抛物线Γ交于另外两个不同的点C、D,则直线CD的斜率k=( )| A. | -$\sqrt{6}$ | B. | -2 | C. | -3 | D. | -$\frac{1}{3}$ |
分析 运用曲线系方程,令参数为0,即可得到所求斜率.
解答 解:由y=3x-2可得y2-(3x-2)2=0,
过直线AB,直线CD和椭圆的曲线系方程为
y2-(3x-2)2+λ(y2-4x)=0,
即(1+λ)y2-9x2+(12-4λ)x-4=0,
令1+λ=-9得λ=-10.此时,曲线表示圆.
令λ=0得y2-(3x-2)2=0,∴y=3x-2和y=-3x+2,
∴直线CD的斜率为-3.
故选C.
点评 本题考查了抛物线的性质,曲线系方程的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.一个算法的程序框图如图所示,该程序输出的结果为$\frac{36}{55}$,则空白处应填入的条件是( )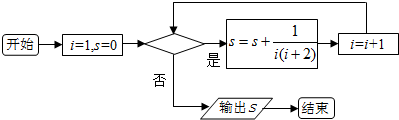

| A. | i≤9 | B. | i≤6 | C. | i≥9 | D. | i≤8 |
2.如图是一个程序框图,则输出s的值是( )


| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
9.tan2016°的值所在的大致区间为( )
| A. | (-1,-$\frac{\sqrt{3}}{3}$) | B. | (-$\frac{\sqrt{3}}{3}$,0) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{3}$,1) |
6.已知iz=2+i,则z的共轭复数在复平面内对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |