题目内容
 已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)求直线PB与平面ABCD所成的角.
考点:直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取PB中点Q,连接MQ、NQ,再加上QN∥BC∥MD,且QN=MD,于是DN∥MQ,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)易证PD⊥MB,又因为底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,然后利用平面与平面垂直的判定定理进行证明;
(3)连结BD,由PD⊥底ABCD,且PD=CD,得∠PBD是直线PB与平面ABCD所成的角,由此能求出直线PB与平面ABCD所成的角.
(2)易证PD⊥MB,又因为底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,然后利用平面与平面垂直的判定定理进行证明;
(3)连结BD,由PD⊥底ABCD,且PD=CD,得∠PBD是直线PB与平面ABCD所成的角,由此能求出直线PB与平面ABCD所成的角.
解答:
 (1)证明:取PB中点Q,连结MQ、NQ,
(1)证明:取PB中点Q,连结MQ、NQ,
∵点M、N分别是棱AD、PC的中点,
∴QN∥BC∥MD,且QN=MD,
∴四边形MQND是平行四边形,∴DN∥MQ,
∵MQ?平面PMB,DN?平面PMB,
∴DN∥平面PMB.
(2)证明:∵PD⊥底ABCD,MB?平面ABCD,
∴PD⊥MB,
又∵底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,
∴MB⊥AD.
又AD∩PD=D,
∴MB⊥平面PAD.
∵MB⊥平面PAD,MB?平面PMB,
∴平面PMB⊥平面PAD.
(3)解:连结BD,
∵底面ABCD是∠A=60°、边长为a的菱形,
∴△ABD是边长为a的等边三角形,
∵PD⊥底ABCD,且PD=CD,
∴∠PBD是直线PB与平面ABCD所成的角,
又Rt△PBD中,PD=BD=a,∠PBD=45°,
∴直线PB与平面ABCD所成的角为45°.
 (1)证明:取PB中点Q,连结MQ、NQ,
(1)证明:取PB中点Q,连结MQ、NQ,∵点M、N分别是棱AD、PC的中点,
∴QN∥BC∥MD,且QN=MD,
∴四边形MQND是平行四边形,∴DN∥MQ,
∵MQ?平面PMB,DN?平面PMB,
∴DN∥平面PMB.
(2)证明:∵PD⊥底ABCD,MB?平面ABCD,
∴PD⊥MB,
又∵底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,
∴MB⊥AD.
又AD∩PD=D,
∴MB⊥平面PAD.
∵MB⊥平面PAD,MB?平面PMB,
∴平面PMB⊥平面PAD.
(3)解:连结BD,
∵底面ABCD是∠A=60°、边长为a的菱形,
∴△ABD是边长为a的等边三角形,
∵PD⊥底ABCD,且PD=CD,
∴∠PBD是直线PB与平面ABCD所成的角,
又Rt△PBD中,PD=BD=a,∠PBD=45°,
∴直线PB与平面ABCD所成的角为45°.
点评:本题主要考查空间线面的位置关系,空间角的计算等基本知识,考查空间想象能力、逻辑思维能力、运算求解能力和探究能力,同时考查学生灵活利用图形,借助向量工具解决问题的能力,考查数形结合思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
集合A={x|y=ln(-x2+2x+3)},B={y|y=ex},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x>-1} |
| D、{x|x<3} |
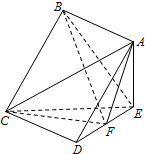 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.