题目内容
【题目】已知点![]() ,椭圆
,椭圆 ![]() 的离心率为
的离心率为![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)利用离心率求出c,再由离心率求出a,结合隐含条件求得b,则椭圆方程可求;(2)当l⊥x轴时不合题意,设l:y=kx-2,联立直线与椭圆的方程,求出P、Q的横坐标,代入弦长公式求得|PQ|,再由点到直线的距离求O到PQ的距离,带入三角形面积公式,换元后利用均值不等式求最值,从而求解.
试题解析:(1)设F(c,0),由条件知, ![]() ,得c=
,得c=![]() .
.
又![]() ,所以a=2,b2=a2-c2=1.
,所以a=2,b2=a2-c2=1.
故E的方程为![]() .
.
(2)当l⊥x轴时不合题意,
故设l:y=kx-2,P(x1,y1),Q(x2,y2).
将y=kx-2代入![]() 中,
中,
得(1+4k2)x2-16kx+12=0.
当Δ=16(4k2-3)>0,即k2>![]() 时,
时,
由根与系数的关系得:
x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
从而|PQ|=![]() |x1-x2|=
|x1-x2|=![]() .
.
又点O到直线PQ的距离d=![]() .
.
所以△OPQ的面积S△OPQ=![]() d·|PQ|=
d·|PQ|=![]() .
.
设![]() =t,则t>0,S△OPQ=
=t,则t>0,S△OPQ=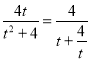 .
.
因为t+![]() ≥4,当且仅当t=2,
≥4,当且仅当t=2,
即k=![]() 时等号成立,且满足Δ>0.
时等号成立,且满足Δ>0.
所以,当△OPQ的面积最大时,l的方程为. ![]() 或
或![]()

练习册系列答案
相关题目