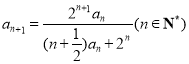题目内容
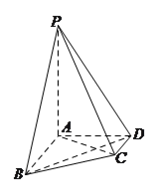
【题目】在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 平面
平面![]() .
.
(1)设平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求证: ![]() .
.
(3)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)利用平行四边形的性质和平行线的传递性即可找出两个平面的交线并且证明结论;(2)利用已知条件结合勾股定理先证明![]() ,再利用线面垂直的性质定理和判定定理即可证明;(3)通过结论空间直角坐标系,设
,再利用线面垂直的性质定理和判定定理即可证明;(3)通过结论空间直角坐标系,设![]() ,利用法向量与斜线所成的角即可找出
,利用法向量与斜线所成的角即可找出![]() 点的位置.
点的位置.
试题解析:(1)如图所示,过点![]() 作
作![]() ,并且取
,并且取![]() ,连接
,连接![]() ,
, ![]()
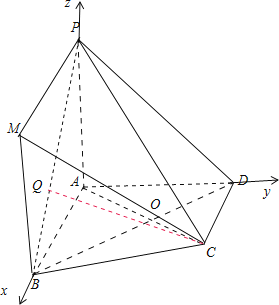
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() 为平面
为平面![]() 平面
平面![]() ,
, ![]() .
.
(2)在![]() 和
和![]() 中,由勾股定理可得
中,由勾股定理可得![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴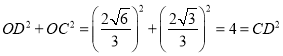 ,∴
,∴![]() ,即
,即![]() ;∵
;∵![]() 底面
底面![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,故
,故![]() .
.
(3)建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() ,∴
,∴![]() ,
, ![]() ,由(2)可知
,由(2)可知![]() 为平面
为平面![]() 的法向量,∴
的法向量,∴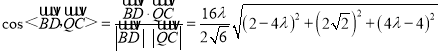 ,∵直线
,∵直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,∴
,∴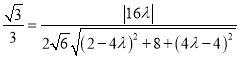 ,化为
,化为![]() ,解得
,解得![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目