题目内容
8.定义min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,若函数f(x)=min{x2-3x+3,-|x-3|+3},且f(x)在区间[m,n]上的值域为[$\frac{3}{4}$,$\frac{7}{4}$],则区间[m,n]长度的最大值为( )| A. | 1 | B. | $\frac{7}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{7}{2}$ |
分析 根据定义作出函数f(x)的解析式和图象,根据函数值域,求出对应点的坐标,利用数形结合进行判断即可.
解答  解:根据定义作出函数f(x)的图象如图:(蓝色曲线),
解:根据定义作出函数f(x)的图象如图:(蓝色曲线),
其中A(1,1),B(3,3),
即f(x)=$\left\{\begin{array}{l}{3-|x-3|,}&{x≤1或x≥3}\\{{x}^{2}-3x+3.}&{1<x<3}\end{array}\right.$,
当f(x)=$\frac{3}{4}$时,当x≥3或x≤1时,由3-|x-3|=$\frac{3}{4}$,得|x-3|=$\frac{9}{4}$,
即xC=$\frac{3}{4}$或xG=$\frac{21}{4}$,
当f(x)=$\frac{7}{4}$时,当1<x<3时,由x2-3x+3=$\frac{7}{4}$,得xE=$\frac{5}{2}$,
由图象知若f(x)在区间[m,n]上的值域为[$\frac{3}{4}$,$\frac{7}{4}$],则区间[m,n]长度的最大值为xF-xC=$\frac{5}{2}$-$\frac{3}{4}$=$\frac{7}{4}$,
故选:B.
点评 本题主要考查函数新定义的应用以及函数值域的求解,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
18.已知函数f(x)=$\frac{1}{3}$x${\;}^{3}-\frac{1}{2}m{x}^{2}+4x-3$在区间[1,2]上是增函数,则实数m的取值范围为( )
| A. | 4≤m≤5 | B. | 2≤m≤4 | C. | m≤2 | D. | m≤4 |
20.已知△ABC中,a,b,c分别为内角A,B,C所对的边长,且a=1,b=$\sqrt{2}$,tanC=1,则△ABC外接圆面积为( )
| A. | $\frac{1}{2}$π | B. | $\frac{1}{3}$π | C. | π | D. | $\sqrt{3}$π |
17.已知集合A={1,2,3},B={0,1,2,4},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,4} | C. | {1,2} | D. | {3} |
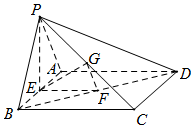 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD. 如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.
如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.