Question

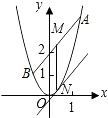
【题目】已知抛物线C：y=2x2 ， 直线y=kx+2交C于A，B两点，M是线段AB的中点，过M作x轴的垂线交C于点N． （Ⅰ）证明：抛物线C在点N处的切线与AB平行；
（Ⅱ）是否存在实数k使 ，若存在，求k的值；若不存在，说明理由．

Answer 1

【答案】解：（Ⅰ）如图，设A（x1 ， 2x12），B（x2 ， 2x22）， 把y=kx+2代入y=2x2得2x2﹣kx﹣2=0，
由韦达定理得 ，x1x2=﹣1，
∴ ，∴N点的坐标为 ．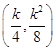
设抛物线在点N处的切线l的方程为 ，
将y=2x2代入上式得 ，
∵直线l与抛物线C相切，
∴ ，
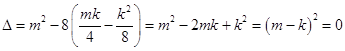∴m=k，即l∥AB．
（Ⅱ）假设存在实数k，使 ，则NA⊥NB，
又∵M是AB的中点，∴ ．
由（Ⅰ）知 = ．
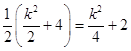∵MN⊥x轴，
∴ ．
又 = ．
∴ ，
解得k=±2．
即存在k=±2，使 ．

【解析】（1）设A（x1 ， 2x12），B（x2 ， 2x22），把直线方程代入抛物线方程消去y，根据韦达定理求得x1+x2和x1x2的值，进而求得N和M的横坐标，表示点M的坐标，设抛物线在点N处的切线l的方程将y=2x2代入进而求得m和k的关系，进而可知l∥AB．（2）假设存在实数k，使 成立，则可知NA⊥NB，又依据M是AB的中点进而可知 ．根据（1）中的条件，分别表示出|MN|和|AB|代入 求得k．