题目内容
【题目】已知 ![]() =(4,5cosα),
=(4,5cosα), ![]() =(3,﹣4tanα)α∈(0,
=(3,﹣4tanα)α∈(0, ![]() ),
), ![]() ⊥
⊥ ![]() .
.
(1)求 ![]() ;
;
(2)求 ![]() .
.
【答案】
(1)解:∵ ![]() ⊥
⊥ ![]() ,
,
∴ ![]() =4×3+5cosα×(﹣4tanα)=12﹣20sinα=0,
=4×3+5cosα×(﹣4tanα)=12﹣20sinα=0,
∴sinα= ![]() ,
,
∵α∈(0, ![]() ),
),
∴ ![]() .
.
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]()
(2)解: 
【解析】(1)由已知利用平面向量垂直的性质可求sinα,进而利用同角三角函数基本关系式可求cosα,tanα的值,进而可求 ![]() ,进而计算得解.(2)利用诱导公式,二倍角的余弦函数公式化简所求结合cosα的值即可计算得解.
,进而计算得解.(2)利用诱导公式,二倍角的余弦函数公式化简所求结合cosα的值即可计算得解.
【考点精析】通过灵活运用数量积判断两个平面向量的垂直关系和两角和与差的正弦公式,掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直;两角和与差的正弦公式:
两平面的法向量垂直;两角和与差的正弦公式:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 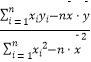 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.

