题目内容
【题目】已知双曲线C1: ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 点M在双曲线C1的一条渐近线上,且OM⊥MF2 , 若△OMF2的面积为16,且双曲线C1与双曲线C2:
=1(a>b>0)的左、右焦点分别为F1 , F2 , 点M在双曲线C1的一条渐近线上,且OM⊥MF2 , 若△OMF2的面积为16,且双曲线C1与双曲线C2: ![]() =1的离心率相同,则双曲线C1的实轴长为( )
=1的离心率相同,则双曲线C1的实轴长为( )
A.32
B.16
C.8
D.4
【答案】B
【解析】解:由双曲线C1: ![]() =1(a>b>0)的一条渐近线为y=
=1(a>b>0)的一条渐近线为y= ![]() x, ∵OM⊥MF2 , F2(c,0),
x, ∵OM⊥MF2 , F2(c,0),
∴丨F2M丨= ![]() =b,
=b,
∵丨OF2丨=c,丨OM丨= ![]() =a△OMF2的面积S=
=a△OMF2的面积S= ![]() 丨F2M丨丨OM丨=
丨F2M丨丨OM丨= ![]() ab=16,则ab=32,
ab=16,则ab=32,
双曲线C2: ![]() =1的离心率e=
=1的离心率e= ![]() =
= ![]() =
= ![]() ,
,
∴e= ![]() =
= ![]() =
= ![]() ,解得:a=8,b=4,
,解得:a=8,b=4,
双曲线C1的实轴长2a=16,
故选B.

 名校课堂系列答案
名校课堂系列答案【题目】某青年教师有一专项课题是进行“学生数学成绩与物理成绩的关系”的研究,他调查了某中学高二年级800名学生上学期期末考试的数学和物理成绩,把成绩按优秀和不优秀分类得到的结果是:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有60人. 附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.
(1)能否在犯错概率不超过0.001的前提下认为该中学学生的数学成绩与物理成绩有关?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取4名学生的成绩,记抽取的4份成绩中数学、物理两科成绩恰有一科优秀的份数为X,求X的分布列和期望E(X).
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 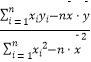 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |

(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.

