题目内容
已知函数f(x)=
的定义域为R,则实数k的取值范围为 .
| kx2+kx+1 |
考点:一元二次不等式的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:根据函数的定义域得到kx2+kx+1≥0恒成立,对k讨论,当k=0,k>0且判别式小于等于0,解不等式即可得到结论.
解答:
解:∵函数f(x)=
的定义域为R,
∴kx2+kx+1≥0恒成立,
当k=0时,不等式等价为1≥0,满足条件;
当k≠0时,要使不等式恒成立,
则
,
即
,
解得0<k≤4,
综上可得0≤k≤4.
故答案为:[0,4].
| kx2+kx+1 |
∴kx2+kx+1≥0恒成立,
当k=0时,不等式等价为1≥0,满足条件;
当k≠0时,要使不等式恒成立,
则
|
即
|
解得0<k≤4,
综上可得0≤k≤4.
故答案为:[0,4].
点评:本题主要考查函数定义域的应用,将函数转化为不等式恒成立是解决本题的关键.注意讨论k=0,属于易错题.

练习册系列答案
相关题目
函数f(x)=1-2sin2x的最小正周期是( )
| A、π | ||
| B、2π | ||
C、
| ||
| D、2 |
已知f(x)=
,则f(
)的值是( )
|
| ||
| 2 |
| A、0 | ||
| B、1 | ||
C、
| ||
D、-
|
函数y=
的定义域为( )
log
|
A、(1,
| ||
B、[1,
| ||
| C、(1,2] | ||
| D、(1,2) |
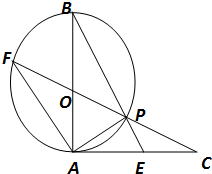 已知:如图,AB是⊙O的直径,AC与⊙O相切于点A,且AC=AB,CO与⊙O相交于点P,CO的延长线与⊙O相交于点F,BP的延长线与AC相交于点E.
已知:如图,AB是⊙O的直径,AC与⊙O相切于点A,且AC=AB,CO与⊙O相交于点P,CO的延长线与⊙O相交于点F,BP的延长线与AC相交于点E.