题目内容
已知函数f（x）=
，若f（x）在R上为非减函数，则实数a的取值范围是 ．
|
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意利用函数的单调性的性质可得
，由此求得a的范围．
|
解答：
解：由题意可得
，由此求得-2≤a≤2
，
故答案为：[-2，2
]．
|
| 3 |
故答案为：[-2，2
| 3 |
点评：本题主要考查函数的单调性的性质，体现了等价转化的数学思想，属于基础题．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
函数f（x）=2x+lgx的零点所在的一个区间是（ ）
A、（0，
| ||
B、（
| ||
| C、（1，2） | ||
| D、（2，+∞） |
设正方形ABCD各顶点的坐标分别为A（-2，-2），B（2，-2），C（2，2），D（-2，2），一束光线从点P（-1，0）出发射到边DC上的点Q（1，2）后反射，然后在正方形内依次经过边CB，AB，AD反射，那么光线第一次回到起点P处所经过的路程为（ ）
A、8
| ||
B、8
| ||
C、4
| ||
| D、10 |
下列数据适合用试验的方法得到的有（ ）
| A、2008年的全国人口总数 |
| B、某学校抽烟的学生在总数中所占的比例 |
| C、某班男生的平均身高 |
| D、顾客对某种产品的满意程度 |
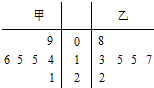甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知角α的顶点在原点，始边与x轴的非负半轴重合，终边过点（-3，4），则sinα的值为（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、-
|