Question

P是双曲线右支上一点（不同于顶点），A、B为左、右焦点，则=________．

Answer 1

分析：作 PH⊥AB，H为垂足，则 sin∠PBA=，sin∠PAB=，面积法求得sin∠APB=，故==，利用双曲线的定义可得答案．
解答：作 PH⊥AB，H为垂足，则 sin∠PBA=，sin∠PAB=．
又AB•PH=PA•PBsin∠APB，∴sin∠APB=，
故=====，
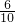故答案为 ．
点评：本题考查双曲线的定义和标准方程，以及双曲线的简单性质的应用，求得sin∠PBA=，sin∠PAB=，sin∠APB=，是解题的关键．