题目内容
已知双曲线的左右焦点是F1,F2,设P是双曲线右支上一点,| F1F2 |
| F1P |
| F1P |
| π |
| 6 |
分析:先根据
在
上的投影的大小恰好为 |
|判断两向量互相垂直得到直角三角形,进而根据直角三角形中内角为
,结合双曲线的定义建立等式求得a和c的关系式,最后根据离心率公式求得离心率e.
| F1F2 |
| F1P |
| F1P |
| π |
| 6 |
解答:解:∵
在
上的投影的大小恰好为 |
|,
∴PF1⊥PF2,
又因为它们的夹角为
,
所以 ∠PF 1F 2=
,
所以在直角三角形PF1F2中,F1F2=2c,
所以PF2=c,PF1=
c
又根据双曲线的定义得:PF1-PF2=2a,
∴
c-c=2a,
∴
=
+1,
所以e=
+1.
故答案为:
+1.
| F1F2 |
| F1P |
| F1P |
∴PF1⊥PF2,
又因为它们的夹角为
| π |
| 6 |
所以 ∠PF 1F 2=
| π |
| 6 |
所以在直角三角形PF1F2中,F1F2=2c,
所以PF2=c,PF1=
| 3 |
又根据双曲线的定义得:PF1-PF2=2a,
∴
| 3 |
∴
| c |
| a |
| 3 |
所以e=
| 3 |
故答案为:
| 3 |
点评:本题主要考查了双曲线的简单性质.考查了学生综合分析问题和运算的能力.解答关键是通过解三角形求得a,c的关系从而求出离心率.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 的左右焦点为
的左右焦点为 ,P为双曲线右支上
,P为双曲线右支上 的最小值为8a,则双曲线的离心率的取值范围是 。
的最小值为8a,则双曲线的离心率的取值范围是 。 的左右焦点分别为
的左右焦点分别为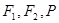 为左支上一点,若
为左支上一点,若 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率 的取值范围为(
)
的取值范围为(
)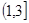 B、
B、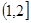 C、
C、 D、
D、
 的左右焦点分别是
的左右焦点分别是 ,
, 点是双曲线右支上一点,且
点是双曲线右支上一点,且 ,则三角形
,则三角形 的面积等于
的面积等于