题目内容
已知函数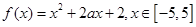
(1)当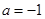 时,求函数的最大值与最小值;
时,求函数的最大值与最小值;
(2)求实数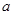 的取值范围,使得
的取值范围,使得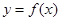 在区间
在区间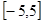 上是单调函数.
上是单调函数.
【答案】
(1) 当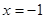 时,函数取得最小值,最小值为1;
时,函数取得最小值,最小值为1;
当 时,函数取得最大值,最大值为
时,函数取得最大值,最大值为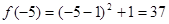 ;
;
(2) 。
。
【解析】本事主要是考查二次函数的性质和单调性的运用。
(1)依题意得当 时,
时, ,那么可知
,那么可知 ,由图象知 当
,由图象知 当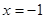 时,函数取得最小值,最小值为1
时,函数取得最小值,最小值为1
(2)由于 图象的对称轴为直线
图象的对称轴为直线 ,根据定语和对称轴的关系得到参数的
范围。
,根据定语和对称轴的关系得到参数的
范围。
解:依题意得
(1)当 时,
时, ,
, 
 2分
2分
若 ,由图象知 当
,由图象知 当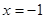 时,函数取得最小值,最小值为1;
时,函数取得最小值,最小值为1;
当 时,函数取得最大值,最大值为
时,函数取得最大值,最大值为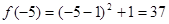 .
. 
 5分
5分
(2)由于 图象的对称轴为直线
图象的对称轴为直线 .
. 
 6分
6分
若函数在
 上为单调增函数,则需要满足
上为单调增函数,则需要满足 即
即 ;
;
 8分
8分
若函数在
 上为单调减函数,则需要满足
上为单调减函数,则需要满足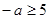 即
即 .
.

 10分
10分
综上,若函数在区间 上为单调函数,则
上为单调函数,则

 12分
12分

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
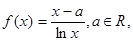
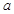 =
=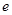 时,求曲线
时,求曲线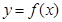 在点(
在点(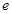 ,
,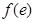 )处的切线方程。
)处的切线方程。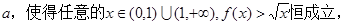 若不存在,说明理由。若存在,求出
若不存在,说明理由。若存在,求出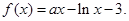
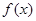 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;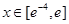 上的图象与直线
上的图象与直线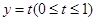 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。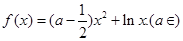
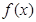 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;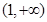 上,函数
上,函数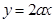 下方,求a的取值范围。
下方,求a的取值范围。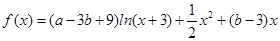 .
.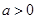 且
且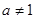 ,
,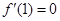 时,试用含
时,试用含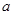 的式子表示
的式子表示 ,并讨论
,并讨论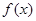 的单调区间;
的单调区间;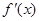 有零点,
有零点,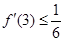 ,且对函数定义域内一切满足
,且对函数定义域内一切满足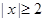 的实数
的实数 有
有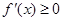 .
. 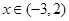 时,求函数
时,求函数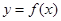 的图象与函数
的图象与函数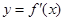 的图象的交点坐标
的图象的交点坐标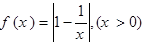
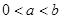 ,且
,且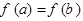 时,求证:
时,求证: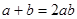
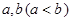 ,使得函数
,使得函数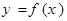 的定义域、值域都是
的定义域、值域都是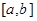 ?若存在,则求出
?若存在,则求出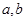 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。