题目内容
13．已知定义在R上的奇函数f（x）满足f（x+3）=-f（x），则f（9）=0．分析 根据条件判断函数的周期性，利用函数奇偶性和周期性的关系将函数值进行转化求解即可．
解答 解：∵f（x+3）=-f（x），
∴f（x+6）=-f（x+3）=f（x），
则函数的周期是6，
则f（9）=f（9-6）=f（3）=-f（0），
∵函数f（x）为奇函数，
∴f（0）=0，则f（9）=-f（0）=0，
故答案为：0．
点评 本题主要考查函数值的计算，根据条件判断函数 的奇偶性和周期性是解决本题的关键．
练习册系列答案
相关题目
19．已知空间向量$\overrightarrow{AB}$，$\overrightarrow{BC}$，$\overrightarrow{CD}$，$\overrightarrow{AD}$，则下列结论正确的是（ ）
| A． | $\overrightarrow{AB}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$ | B． | $\overrightarrow{AB}$-$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\overrightarrow{AD}$ | C． | $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{DC}$ | D． | $\overrightarrow{BC}$=$\overrightarrow{BD}$-$\overrightarrow{DC}$ |
1．已知不共线向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{AB}$=t$\overrightarrow{a}$-$\overrightarrow{b}$（t∈R），$\overrightarrow{AC}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$，若A，B，C三点共线，则实数t=（ ）
| A． | -$\frac{1}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
8．已知集合A={1，2，3}，B={2，3，5}，则A∩B=（ ）
| A． | {1，5} | B． | {1，2，5} | C． | {2，3} | D． | {1，2，3，5} |
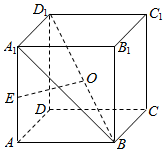如图，在正方体ABCD-A1B1C1D1中，AA1=2，E为AA1的中点，O是BD1的中点．