题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点.
上的两个不同点.
(1)若![]() ,且点
,且点![]() 所在直线方程为
所在直线方程为![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,线段
,线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接
,连接![]() 并廷长交椭圆
并廷长交椭圆![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() ,由
,由![]() 得
得![]() ,化简得
,化简得![]() ,联立直线方程与椭圆方程,利用韦达定理代入化简得
,联立直线方程与椭圆方程,利用韦达定理代入化简得![]() 的值;(2)根据条件得
的值;(2)根据条件得![]() ,设
,设![]() ,则得点
,则得点![]() ,代入椭圆方程,利用
,代入椭圆方程,利用![]() ,
, ![]() ,以及由直线
,以及由直线![]() 斜率之积为
斜率之积为![]() ,得
,得![]() ,代入化简可得
,代入化简可得![]() 的值.
的值.
试题解析:(1)由题知![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
设![]() ,将直线
,将直线![]() 代入椭圆方程得:
代入椭圆方程得:![]() ,
,
∴由韦达定理知:![]() .
.
∵![]() ,∴
,∴![]() ,即
,即
![]() ,
,
将![]() 代入得
代入得![]() ,即
,即![]() ,
,
解得![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
(2)设![]() ,
,![]() ,
,
由题知![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵![]() ,∴
,∴![]() ,即
,即
![]() .
.
∵点![]() 在椭圆
在椭圆![]() 上,∴
上,∴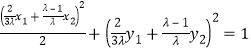 ,
,
即![]() .
.![]()
∵![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,①
,① ![]() ,②
,②
又直线![]() 斜率之积为
斜率之积为![]() ,∴
,∴![]() ,即
,即![]() ,③
,③
将①②③代入![]() 得
得![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目
【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024/span> | 6.635 | 7.879 | 10.828 |