题目内容
20.不等式$\sqrt{{-x}^{2}-4x}$≤$\frac{4}{3}$x+1-a的解集是[-4,0].则a的取值范围是(-∞,-5].分析 令y=$\sqrt{{-x}^{2}-4x}$,即(x+2)2+y2=4(y≥0),它表示一个以C(-2,0)为圆心、半径等于2的半圆,则由题意可得,当x∈[-4,0]时,半圆y=$\sqrt{{-x}^{2}-4x}$ 不能在直线y=$\frac{4}{3}$x+1-a的上方.当直线l和半圆相切时,求得a的值,数形结合求得a的范围.
解答 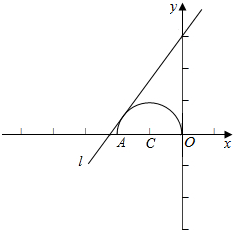 解:不等式$\sqrt{{-x}^{2}-4x}$≤$\frac{4}{3}$x+1-a的解集是[-4,0],
解:不等式$\sqrt{{-x}^{2}-4x}$≤$\frac{4}{3}$x+1-a的解集是[-4,0],
令y=$\sqrt{{-x}^{2}-4x}$,即:(x+2)2+y2=4(y≥0),它表示一个以C(-2,0)为圆心、
半径等于2的半圆,如图所示:
则由题意可得,当x∈[-4,0]时,半圆y=$\sqrt{{-x}^{2}-4x}$ 不能在直线y=$\frac{4}{3}$x+1-a的上方.
当直线l和半圆相切时,
根据圆心C(-2,0)到直线l:y=$\frac{4}{3}$x+1-a的距离等于半径,
可得$\frac{|-\frac{8}{3}-0+1-a|}{\sqrt{\frac{16}{9}+1}}$=2,求得a=$\frac{5}{3}$,或a=-5.
由于直线l在y轴上的截距为1-a,数形结合可得,应取a=-5.
故当半圆y=$\sqrt{{-x}^{2}-4x}$ 在直线y=$\frac{4}{3}$x+1-a的下方时,
应把此切线l向上平移,即直线l在y轴上的截距应该变大,即1-a变大,故有a≤-5,
故答案为:(-∞,-5].
点评 本题主要考查圆的标准方程,直线和圆的位置关系、点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目
8.f(x)为定义域R,图象关于原点对称,当x≥0时,f(x)=2x+2x+b(b为常数),则x<0时,f(x)解析式为( )
| A. | f(x)=2x-2x-1 | B. | f(x)=-2-x+2x+1 | C. | f(x)=2-x-2x-1 | D. | f(x)=-2-x-2x+1 |
10.“m=1”是“函数f(x)=log2(1+mx)+log2(1-x)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |