题目内容
已知cos(π+α)=
,α∈(π,
),则tanα= .
| 3 |
| 5 |
| 3π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式左边利用诱导公式化简求出cosα的值,根据α的范围,利用同角三角函数间基本关系求出sinα的值,即可确定出tanα的值.
解答:
解:∵cos(π+α)=-cosα=
,α∈(π,
),
∴cosα=-
,sinα=-
=-
,
则tanα=
=
.
故答案为:
.
| 3 |
| 5 |
| 3π |
| 2 |
∴cosα=-
| 3 |
| 5 |
| 1-cos2α |
| 4 |
| 5 |
则tanα=
| sinα |
| cosα |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
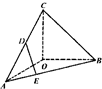 如图,在四面体ABCD中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=
如图,在四面体ABCD中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=
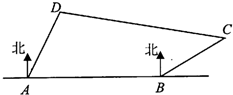 如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3
如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3