题目内容
若圆锥的母线为
,底面面积为π,则该圆锥的体积为 .
| 2 |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:圆锥的底面面积,求出底面半径,然后求出圆锥的高,即可求出圆锥的体积.
解答:
解:∵圆锥的底面面积为π,
∴圆锥的底面半径r=1;
又∵圆锥的母线长l=
,
圆锥的高h=
=1,
所以圆锥的体积V=
πr2h=
π,
故答案为:
.
∴圆锥的底面半径r=1;
又∵圆锥的母线长l=
| 2 |
圆锥的高h=
(
|
所以圆锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:
| π |
| 3 |
点评:本题是中档题,考查计算能力,圆锥的高的求法,底面半径的求法,是必得分的题目.

练习册系列答案
相关题目
下列推理过程是演绎推理的是( )
| A、由平面三角形的性质推测空间三棱锥的性质 |
| B、某校高二1班有55人,2班有52人,由此得高二所有班人数都超过50人 |
| C、两条直线平行,同位角相等;若∠A与∠B是两条平行直线的同位角,则∠A=∠B |
| D、在数列{an}中,a1=2,an=2an-1+1(n≥2),由此归纳出{an}的通项公式 |
 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示,关于该四棱锥的下列结论中:
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示,关于该四棱锥的下列结论中: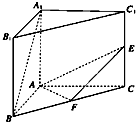 设在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F依次为C1C,BC的中点.则异面直线A1B、EF所成角θ的大小
设在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F依次为C1C,BC的中点.则异面直线A1B、EF所成角θ的大小