Question

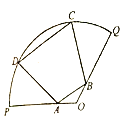
【题目】为丰富市民的文化生活，市政府计划在一块半径为200m，圆心角为的扇形地上建造市民广场，规划设计如图：内接梯形区域为运动休闲区，其中A，B分别在半径，上，C，D在圆弧上，

；上，；区域为文化展区，长为，其余空地为绿化区域，且长不得超过200m.

(1)试确定A，B的位置，使的周长最大？

(2)当的周长最长时，设，试将运动休闲区的面积S表示为的函数，并求出S的最大值.

Answer 1

【答案】（1）、都为50m；（2）；；最大值为.

【解析】

对于（1），设，，m，，在△OAB中，利用余弦定理可得，整理得，结合基本不等式即可得出结论；

对于（2），当△AOB的周长最大时，梯形ACBD为等腰梯形，过O作OF⊥CD交CD于F，交AB于E，则E、F分别为AB，CD的中点，利用已知可表示出相关线段；然后利用梯形的面积公式可知， ，，令，，，结合导数，确定函数的单调性，即可求出S的最大值。

解：（1）设，，m，，

在中，，

即.

所以.

所以，当且仅当时，取得最大值，

此时周长取得最大值.

答：当、都为50m时，的周长最大.

（2）当的周长最大时，梯形为等腰梯形.

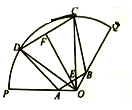
如上图所示，过O作交于F，交于E，则E、F分别为、的中点，

所以.由，得.

在中，，.

又在中，，故.

所以

，.

令，，

，.

又及在上均为单调递减函数，

故在上为单调递减函数.

因，故在上恒成立，

于是，在上为单调递增函数.

所以当时，有最大值，此时S有最大值为.

答：当时，梯形面积有最大值，且最大值为.