题目内容
已知函数 ,m∈R,且
,m∈R,且 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若 +,且
+,且 ,求
,求 的最小值.
的最小值.
(1) .(2)
.(2) 的最小值为9.
的最小值为9.
解析试题分析:(1)由已知 ,得到
,得到
所以
根据 的解集是
的解集是 ,得到
,得到 .
.
(2)由(1)知 ,
, ,由柯西不等式即得所求.
,由柯西不等式即得所求.
试题解析:(1)因为 ,所以
,所以 .
.
所以
又 的解集是
的解集是 ,故
,故 . 5分
. 5分
(2)由(1)知 ,
, ,由柯西不等式得
,由柯西不等式得
∴ 的最小值为9 10分
的最小值为9 10分
考点:绝对值不等式解法,柯西不等式.

练习册系列答案
相关题目
 , 解关于
, 解关于 的不等式
的不等式 
 的解集是
的解集是 ,求实数
,求实数 的值
的值 ,求证:a>b.
,求证:a>b.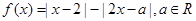 .
.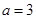 时,解不等式
时,解不等式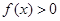 ;
;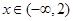 时,
时,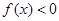 恒成立,求
恒成立,求 的取值范围.
的取值范围.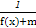 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
 ,求证:
,求证: .
. ,求x+y+z的值.
,求x+y+z的值.