题目内容
6.命题:“?x∈[0,+∞),x3+2x≥0”的否定是( )| A. | ?x∈(-∞,0),x3+2x<0 | B. | ?x∈[0,+∞),x3+2x<0 | C. | ?x∈(-∞,0),x3+2x≥0 | D. | ?x∈[0,+∞),x3+2x≥0 |
分析 由全称命题的否定的规则可得.
解答 解:∵命题:“?x∈[0,+∞),x3+2x≥0”为全称命题,
故其否定为特称命题,排除A和C,
再由否定的规则可得:“?x∈[0,+∞),x3+2x<0”
故选:B.
点评 本题考查全称命题的否定,属基础题.

练习册系列答案
相关题目
17.与二进制数110(2)相等的十进制数是( )
| A. | 6 | B. | 7 | C. | 10 | D. | 11 |
15.已知集合A={x|log2(x-4)≤0},B={y|y=ax+1(a>0且a≠1)},则(∁RA)∩B=( )
| A. | (5,+∞) | B. | (1,4]∪(5,+∞) | C. | [1,4)∪[5,+∞) | D. | [1,4) |
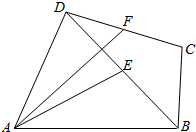 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.