题目内容
6.已知四边形ABCD,∠A=∠C=90°,∠B=60°,AC=$\sqrt{15}$,求BD的长.分析 以BD为直径做圆O,则A,B,C,D四点共圆,连结OA,OC,在△AOC中使用余弦定理求出圆的半径,继而得到直径的长.
解答  解:以BD为直径做圆O,∵∠A=∠C=90°,∴A,C在圆O上,连结OA,OC,
解:以BD为直径做圆O,∵∠A=∠C=90°,∴A,C在圆O上,连结OA,OC,
∵∠B=60°,∴∠AOC=120°,
设圆O半径为r,则OA=OC=r,BD=2r.
在△AOC中,由余弦定理得AC2=OA2+OC2-2OA•OCcos120°,
即r2+r2+r2=15,∴r=$\sqrt{5}$.
∴BD=2r=2$\sqrt{5}$.
点评 本题考查了余弦定理的应用,作出辅助圆是解题关键.

练习册系列答案
相关题目
1.如图所示,在正面体ABCD-A1B1C1D1中,AD1∩A1D=O,则线段CO在平面AD1内的射影是( )
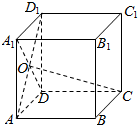

| A. | 线段DO | B. | 线段D1O | C. | 线段A1O | D. | 线段AO |
18.若AB∥A′B′,AC∥A′C′,则有( )
| A. | ∠BAC=∠B′A′C′ | |
| B. | ∠BAC+∠B′A′C′=180° | |
| C. | ∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180° | |
| D. | ∠BAC>∠B′A′C′ |
15.函数f(x)=$\sqrt{{x}^{2}}$是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
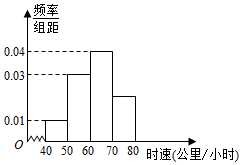 已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.
已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.