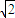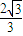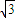题目内容
已知双曲线 的焦点F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为
的焦点F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为
- A.
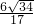
- B.
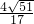
- C.

- D.

C
分析:由题意可得点M的横坐标为-c=-2,代入双曲线方程可得 y=±3,故MF1=3,又 F1F2=2c=4,利用面积法求直角三角形斜边上的高.
解答:由题意可得点M的横坐标为-c=-2,代入双曲线方程可得 y=±3,
∴MF1=3,F1F2=2c=4,
直角三角形MF1F2中,F1到直线F2M的距离为h= =
= =
= ,
,
故选 C.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,利用面积法求直角三角形斜边上的高.
分析:由题意可得点M的横坐标为-c=-2,代入双曲线方程可得 y=±3,故MF1=3,又 F1F2=2c=4,利用面积法求直角三角形斜边上的高.
解答:由题意可得点M的横坐标为-c=-2,代入双曲线方程可得 y=±3,
∴MF1=3,F1F2=2c=4,
直角三角形MF1F2中,F1到直线F2M的距离为h=
 =
= =
= ,
,故选 C.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,利用面积法求直角三角形斜边上的高.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ,且过点
,且过点 ;
; 有共同的渐近线,且经过点
有共同的渐近线,且经过点 .
.