题目内容
【题目】已知F1、F2分别是双曲线
1（a＞0，b＞0）的左、右焦点，若双曲线的右支上存在一点P，使得（
）
0（O为坐标原点），且|PF1|
|PF2|，则双曲线的离心率的取值范围是_____．
【答案】
【解析】
由
0，可得（
）（
）＝0，即|OP|＝c，则∠F1PF2＝90°，设|PF1|＝m，|PF2|＝n，可得m﹣n＝2a，且m2+n2＝4c2，令m=kn，结合双曲线定义及不等式求得e的范围从而求得结果.
0，即为（）（）＝0，
即为
2
2，可得|OP|＝c，
即有∠F1PF2＝90°，设|PF1|＝m，|PF2|＝n，可得m﹣n＝2a，
且m2+n2＝4c2，令m=kn，
∴n
，m
．
△PF1F2中，由勾股定理得|PF1|2+|PF2|2＝4c2，
∴（
）2+（
）2＝4c2，
∴（
）2+（
）2＝e2，又k
，
e2=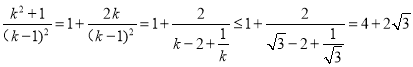
，
即有，
故答案为：.
练习册系列答案
相关题目
