题目内容
10.某市为了解各校《国学》课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A、B、C、D四个等级,随机调阅了甲、乙两所学校各60名学生的成绩,得到如图所示分布图:
(Ⅰ)试确定图中实数a与b的值;
(Ⅱ)规定等级D为“不合格”,其他等级为“合格”,以事件发生的频率作为相应事件发生的概率,若从甲、乙两校“合格”的学生中各选1名学生,求甲校学生成绩高于乙校学生成绩的概率.
分析 (Ⅰ)利用条形图,即可确定图中实数a与b的值;
(Ⅱ)利用互斥事件的概率公式,即可求甲校学生成绩高于乙校学生成绩的概率.
解答 解:(Ⅰ)由题意,6+a+33+6=60,∴a=15.
0.15+b+0.2+0.15=1,∴b=0.5;
(Ⅱ)设E1表示“甲校学生成绩等级为A”,则P(E1)=$\frac{6}{54}$,E2表示“甲校学生成绩等级为B”,则P(E2)=$\frac{15}{54}$,F1表示“乙校学生成绩等级为B或C”,则P(F1)=$\frac{42}{51}$,F2表示“乙校学生成绩等级为C”,
则P(F2)=$\frac{12}{51}$,∴甲校学生成绩高于乙校学生成绩的概率为$\frac{6}{54}×\frac{42}{51}$+$\frac{15}{54}×\frac{12}{51}$=$\frac{8}{51}$.
点评 本题考查条形图,考查概率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
1.设圆x2+y2-2x-2y-2=0的圆心为C,直线l过(0,3)与圆C交于A,B两点,若$|{AB}|=2\sqrt{3}$,则直线l的方程为( )
| A. | 3x+4y-12=0或4x-3y+9=0 | B. | 3x+4y-12=0或x=0 | ||
| C. | 4x-3y+9=0或x=0 | D. | 3x-4y+12=0或4x+3y+9=0 |
18.已知$\left\{\begin{array}{l}x+2y≥2\\ 3x-y-6≤0\\ 2x-3y+3≥0\end{array}\right.$,且z=x2+y2,则z的最小值是( )
| A. | 4 | B. | 1 | C. | 18 | D. | $\frac{4}{5}$ |
15.设函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0)的最小正周期为π,则“f(-x)=f(x)”是“φ=$\frac{π}{4}$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知函数f(x)=$\left\{\begin{array}{l}{3x+3(x≤-1)}\\{f(x-1)+1(x>-1)}\end{array}\right.$方程f(x)=x+1的解从小到大排成一个数列{an},该数列的前n项的和为Sn,则$\frac{2{S}_{n+3}+10}{n}$的最小值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
20.把函数$f(x)=\sqrt{2}sin(2x-\frac{π}{4})$的图象上每个点的横坐标扩大到原来的4倍,再向左平移$\frac{π}{3}$,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
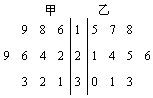 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.