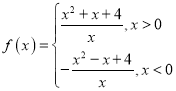题目内容
【题目】某生物研究者于元旦在湖中放入一些凤眼莲,这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲覆盖面积为![]() ,三月底测得凤眼莲覆盖面积为
,三月底测得凤眼莲覆盖面积为![]() ,凤眼莲覆盖面积
,凤眼莲覆盖面积![]() (单位:
(单位:![]() )与月份
)与月份![]() (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适并求出该模型的解析式;
(2)求凤眼莲覆盖面积是元旦放入面积![]() 倍以上的最小月份.
倍以上的最小月份.
(参考数据![]() ,
,![]() )
)
【答案】(1) 模型![]() 更适合,解析式为
更适合,解析式为
(2)最小为6月份
【解析】
(1)由凤眼莲在湖中的蔓延速度越来越快判断即可.
(2)利用在元旦时,![]() ,
,![]() ,再列出表达式求解不等式即可.
,再列出表达式求解不等式即可.
(1)两个函数![]() ,
,![]() 在
在![]() 上都是增函数,随着
上都是增函数,随着![]() 的增加,函数
的增加,函数![]() 的值增加的越来越快,而函数
的值增加的越来越快,而函数![]() 的值增加的越来越慢,由于凤眼莲在湖中的蔓延速度越来越快,所以函数模型
的值增加的越来越慢,由于凤眼莲在湖中的蔓延速度越来越快,所以函数模型![]() 适合要求.
适合要求.
由题意可知,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,所以
,所以 ,解得
,解得
所以该函数模型的解析式是
(2) ![]() 时,
时,![]() ,所以元旦放入凤眼莲面积是
,所以元旦放入凤眼莲面积是![]() ,
,
由 得
得 所以
所以 ,
,
因为![]() ,所以
,所以![]() ,
,
所以凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是6月份.

练习册系列答案
相关题目
【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.