题目内容
19.已知全集U=R,且A={x||x-2|>2},B={x|y=$\frac{1}{\sqrt{-{x}^{2}+2x+3}}$},则(∁UA)∩B等于( )| A. | (-1,3) | B. | (-1,0)∪(3,4) | C. | (3,4) | D. | [0,3) |
分析 分别求解一元二次不等式和绝对值的不等式化简集合A与B,求出A的补集,然后利用交集运算求解.
解答 解:A={x||x-2|>2}=(-∞,0)∪(4,+∞),
∴∁UA=[0,4]
由B={x|y=$\frac{1}{\sqrt{-{x}^{2}+2x+3}}$},
∴-x2+2x+3>0,解得-1<x<3,
∴B=(-1,3),
∴(∁UA)∩B=[0,3),
故选:D
点评 本题考查了交、并、补集的混合运算,考查了一元二次不等式和绝对值不等式的解法,是基础的运算题.

练习册系列答案
相关题目
9.圆(x-3)2+(y+4)2=1关于y2=8x轴对称的圆的方程是( )
| A. | (x+3)2+(y+4)2=1 | B. | (x-4)2+(y+3)2=1 | C. | (x+4)2+(y-3)2=1 | D. | (x-3)2+(y-4)2=1 |
14. 如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )
如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )
 如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )
如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
4.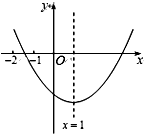 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表资料:
(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$(其中已计算出$\widehat{b}$=$\frac{5}{2}$);
(2)若由线性回归方程得到的估计数据与所选出的检验数据(选取的检验数据是12月1日与12月5日
的两组数据)的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据(选取的检验数据是12月1日与12月5日
的两组数据)的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
8.已知|$\overrightarrow a$|=4cos$\frac{π}{8}$,|$\overrightarrow b$|=2sin$\frac{π}{8}$,$\overrightarrow a$•$\overrightarrow b$=-$\sqrt{2}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
9.设a=log0.32,b=ln2,c=5${\;}^{\frac{1}{2}}}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |