题目内容
某工厂组织工人参加上岗测试，每位测试者最多有三次机会，一旦某次测试通过，便可上岗工作，不再参加以后的测试；否则就再测试直到第三次为止．设每位工人每次测试通过的概率依次为
、
、．
（Ⅰ）若有4位工人参加上岗测试，求恰有2人通过测试的概率；
（Ⅱ）求工人甲在上岗测试中参加测试次数ξ的分布列及Eξ．
解：（Ⅰ）设“每位工人通过上岗测试”为事件A，
则
．
[或
∴4位工人中恰有2人通过测试的概率为
．
（Ⅱ）ξ的取值为1、2、3．
，
，
．
故工人甲在上岗测试中参加测试次数ξ的分布列为
∴
．
分析：（Ⅰ）每位工人每次测试通过的概率都相同，所以服从二项分布．4位工人参加上岗测试，求恰有2人通过测试的概率，套公式即可．
（Ⅱ）参加测试次数ξ的所有可能取值为1、2、3，求出相应的概率，画出分布列并求出数学期望．
点评：此题考查二项分布的理解与求法及离散型随机变量的分布列和期望．
则
．[或
∴4位工人中恰有2人通过测试的概率为
．（Ⅱ）ξ的取值为1、2、3．
，，．故工人甲在上岗测试中参加测试次数ξ的分布列为
∴
．分析：（Ⅰ）每位工人每次测试通过的概率都相同，所以服从二项分布．4位工人参加上岗测试，求恰有2人通过测试的概率，套公式即可．
（Ⅱ）参加测试次数ξ的所有可能取值为1、2、3，求出相应的概率，画出分布列并求出数学期望．
点评：此题考查二项分布的理解与求法及离散型随机变量的分布列和期望．
练习册系列答案
相关题目
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”．为提高公众对健康睡眠的科学认识和自我管理能力，某网站于3月13日起进行了为期一周的在线调查，共有200人参与．现将数据整理分组如表所示．
（1）画出频率分布直方图；
（2）调查对象中睡眠时间少于8的频率是多少？
（3）为了对数据进行分析，采用了计算机辅助计算，算法流程如图所示．求输出的S的值，并说明S的统计意义．
| 序号i | 分组睡眠时间（小时） | 组中值（m1） | 频数（人数） | 频率（f1） |
| 1 | [4，5） | 4.5 | 8 | 0.04 |
| 2 | [5，6） | 5.5 | 52 | 0.26 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.28 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10） | 9.5 | 4 | 0.02 |
，且它的一个焦点与抛物线y2=8x的焦点重合，则此椭圆方程为
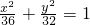
在区间（0，2）上的实根个数共有
，乙每次投中的概率为