题目内容
12．“x＜1”是“x＜2”的充分不必要条件．分析 根据充分本题条件的定义结合集合的包含关系判断即可．
解答 解：由题意x＜1能推出x＜2，是充分条件，
反之不成立，不是必要条件，
故答案为：充分不必要．
点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20．函数f（x）=$\frac{1}{2}$x2-lnx，在（1，$\frac{1}{2}$）处的切线斜率为（ ）
| A． | 1 | B． | 2 | C． | 0 | D． | $\frac{1}{2}$ |
20．设集合A={1，2，3，4}，则集合A的真子集的个数为（ ）
| A． | 16 | B． | 15 | C． | 14 | D． | 13 |
4．若不等式x2+x+a+1≥0对一切$x∈[{0，\frac{1}{2}}]$都成立，则a的最小值为（ ）
| A． | 0 | B． | -1 | C． | $-\frac{5}{2}$ | D． | $-\frac{7}{4}$ |
1．已知某随机变量X的概率密度函数为$P（x）=\left\{\begin{array}{l}0，x≠0\\{e^{-x}}，x＞0\end{array}\right.$，则随机变量X落在区间（1，3）内的概率为（ ）
| A． | $\frac{e+1}{e^2}$ | B． | $\frac{{{e^2}-1}}{e^3}$ | C． | e2-e | D． | e2+e |
2．
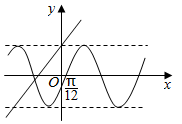若函数y=ksin（kx+φ）（k＞0，|φ|＜$\frac{π}{2}$）与函数y=kx-k2+6的部分图象如图所示，则函数f（x）=sin（kx-φ）+cos（kx-φ）图象的一条对称轴的方程可以为（ ）
若函数y=ksin（kx+φ）（k＞0，|φ|＜$\frac{π}{2}$）与函数y=kx-k2+6的部分图象如图所示，则函数f（x）=sin（kx-φ）+cos（kx-φ）图象的一条对称轴的方程可以为（ ）| A． | x=-$\frac{π}{24}$ | B． | x=$\frac{37π}{24}$ | C． | x=$\frac{17π}{24}$ | D． | x=-$\frac{13π}{24}$ |