题目内容
定义域为{x|x≠0}的函数f(x)满足f(xy)=f(x)+f(y),(x,y∈R)且f(8)=3,则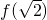 =
=
- A.

- B.

- C.

- D.

A
分析:根据题意可得f(8)=3f(2)=6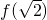 ,从而求得
,从而求得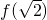 的值.
的值.
解答:∵函数f(x)满足f(xy)=f(x)+f(y),(x,y∈R)且f(8)=3,
∴f(8)=f(4)+f(2)=3f(2)=3 ( )=6
)=6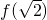 =3,
=3,
∴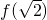 =
= ,
,
故选A.
点评:本题考查根据函数的性质求函数的值,得到f(8)=3f(2)=6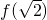 ,是解题的关键.
,是解题的关键.
分析:根据题意可得f(8)=3f(2)=6
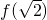 ,从而求得
,从而求得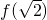 的值.
的值.解答:∵函数f(x)满足f(xy)=f(x)+f(y),(x,y∈R)且f(8)=3,
∴f(8)=f(4)+f(2)=3f(2)=3 (
 )=6
)=6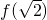 =3,
=3,∴
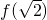 =
= ,
,故选A.
点评:本题考查根据函数的性质求函数的值,得到f(8)=3f(2)=6
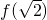 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 如图,已知奇函数f(x)的定义域为{x|x≠0,x∈R},且f(3)=0则不等式
如图,已知奇函数f(x)的定义域为{x|x≠0,x∈R},且f(3)=0则不等式