题目内容
已知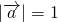 ,
,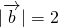 ,
, 的夹角为
的夹角为 ,试求:
,试求:
(1) +
+ 与
与 -
- 夹角的余弦值.
夹角的余弦值.
(2)使向量 +λ
+λ 与λ
与λ -
- 的夹角为钝角时,λ的取值范围.
的夹角为钝角时,λ的取值范围.
解:∵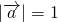 ,
,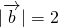 ,
,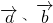 的夹角为
的夹角为 ,
,
∴ =
=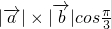 =1
=1
(1)∵( +
+ )2=
)2= +2
+2 +
+ =1+2×1+4=7,(
=1+2×1+4=7,( -
- )2=
)2= -2
-2 +
+ =1-2×1+4=3,
=1-2×1+4=3,
∴| +
+ |=
|= ,|
,| -
- |=
|=
设 +
+ 与
与 -
- 的夹角为α,则
的夹角为α,则
cosα=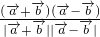 =
=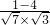 =-
=-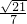 ,
,
即 +
+ 与
与 -
- 夹角的余弦值等于-
夹角的余弦值等于-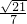
(2)根据题意,不存在λ值,使向量 +λ
+λ 与λ
与λ -
- 的夹角为π,
的夹角为π,
∴向量 +λ
+λ 与λ
与λ -
- 的夹角为钝角时,可得
的夹角为钝角时,可得
( +λ
+λ )(λ
)(λ -
- )<0,即λ
)<0,即λ +(λ2-1)
+(λ2-1) -λ
-λ <0
<0
将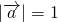 ,
,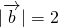 和
和 =1代入,可得
=1代入,可得
λ+(λ2-1)-4λ<0,整理得λ2-3λ-1<0
解这个不等式,得 <λ<
<λ<
因此λ的取值范围是( ,
, ).
).
分析:(1)由向量数量积公式,算出 =1,从而得到|
=1,从而得到| +
+ |=
|= ,|
,| -
- |=
|= .最后用向量的夹角公式,即可得到
.最后用向量的夹角公式,即可得到 +
+ 与
与 -
- 夹角的余弦值.
夹角的余弦值.
(2)根据题意,得向量 +λ
+λ 与λ
与λ -
- 的数量积为负数,因此计算
的数量积为负数,因此计算 +λ
+λ 与λ
与λ -
- 的数量积并代入题中的数据,得到关于λ的一元二次不等式,解之即可得到实数λ的取值范围.
的数量积并代入题中的数据,得到关于λ的一元二次不等式,解之即可得到实数λ的取值范围.
点评:本题给出两个向量的模与夹角,求它们和向量与差向量夹角的大小,并讨论向量夹角为钝角的问题,着重考查了平面向量的数量积及其运算性质等知识,属于基础题.
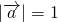 ,
,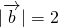 ,
,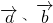 的夹角为
的夹角为 ,
,∴
 =
=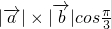 =1
=1(1)∵(
 +
+ )2=
)2= +2
+2 +
+ =1+2×1+4=7,(
=1+2×1+4=7,( -
- )2=
)2= -2
-2 +
+ =1-2×1+4=3,
=1-2×1+4=3,∴|
 +
+ |=
|= ,|
,| -
- |=
|=
设
 +
+ 与
与 -
- 的夹角为α,则
的夹角为α,则cosα=
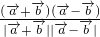 =
=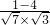 =-
=-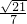 ,
,即
 +
+ 与
与 -
- 夹角的余弦值等于-
夹角的余弦值等于-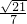
(2)根据题意,不存在λ值,使向量
 +λ
+λ 与λ
与λ -
- 的夹角为π,
的夹角为π,∴向量
 +λ
+λ 与λ
与λ -
- 的夹角为钝角时,可得
的夹角为钝角时,可得(
 +λ
+λ )(λ
)(λ -
- )<0,即λ
)<0,即λ +(λ2-1)
+(λ2-1) -λ
-λ <0
<0将
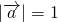 ,
,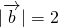 和
和 =1代入,可得
=1代入,可得λ+(λ2-1)-4λ<0,整理得λ2-3λ-1<0
解这个不等式,得
 <λ<
<λ<
因此λ的取值范围是(
 ,
, ).
).分析:(1)由向量数量积公式,算出
 =1,从而得到|
=1,从而得到| +
+ |=
|= ,|
,| -
- |=
|= .最后用向量的夹角公式,即可得到
.最后用向量的夹角公式,即可得到 +
+ 与
与 -
- 夹角的余弦值.
夹角的余弦值.(2)根据题意,得向量
 +λ
+λ 与λ
与λ -
- 的数量积为负数,因此计算
的数量积为负数,因此计算 +λ
+λ 与λ
与λ -
- 的数量积并代入题中的数据,得到关于λ的一元二次不等式,解之即可得到实数λ的取值范围.
的数量积并代入题中的数据,得到关于λ的一元二次不等式,解之即可得到实数λ的取值范围.点评:本题给出两个向量的模与夹角,求它们和向量与差向量夹角的大小,并讨论向量夹角为钝角的问题,着重考查了平面向量的数量积及其运算性质等知识,属于基础题.

练习册系列答案
相关题目
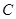 城周边已有两条公路
城周边已有两条公路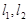 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为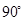 .已知
.已知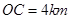 ,
, 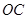 与公路
与公路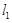 夹角为
夹角为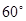 .现规划在公路
.现规划在公路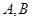 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过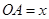
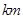 ,
,
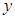 关于
关于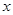 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域;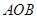 的面积最小.
的面积最小.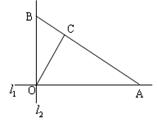
 ,设
,设 ,
,
 的值;(3)若
的值;(3)若 与
与 的夹角为钝角,试求实数t的取值范围.
的夹角为钝角,试求实数t的取值范围.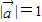 ,
,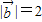 ,
,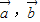 的夹角为
的夹角为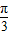 ,试求:
,试求: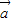 +
+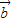 与
与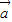 -
-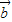 夹角的余弦值.
夹角的余弦值.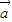 +λ
+λ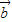 与λ
与λ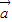 -
-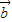 的夹角为钝角时,λ的取值范围.
的夹角为钝角时,λ的取值范围.