题目内容
3.已知f(x)是定义在[-1,1]上的奇函数,f(1)=1,且若?a、b∈[-1,1],a+b≠0,恒有$\frac{f(a)+f(b)}{a+b}$>0,(1)证明:函数f(x)在[-1,1]上是增函数;
(2)若?x∈[-1,1],对?a∈[-1,1],不等式f(x)≥m2-2am-2恒成立,求实数m的取值范围.
分析 (1)任取x1、x2∈[-1,1],且x1<x2,根据已知判断f(x1)-f(x2)的符号,结合增函数的定义,可得函数f(x)在[-1,1]上是增函数;
(2)若?x∈[-1,1],对?a∈[-1,1],不等式f(x)≥m2-2am-2恒成立,只须f(x)max≥m2-2am-2,进而得到实数m的取值范围.
解答 (1)证明:任取x1、x2∈[-1,1],且x1<x2,
则f(x1)-f(x2)=f(x1)+f(-x2)
∵$\frac{f({x}_{1})+f(-{x}_{2})}{{x}_{1}-{x}_{2}}$>0,
即$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
∵x1-x2<0,
∴f(x1)-f(x2)<0.则f(x)是[-1,1]上的增函数;
(2)要使存在x∈[-1,1],使f(x)≥m2-2am-2对所有a∈[-1,1]恒成立,
只须f(x)max≥m2-2am-2,即1≥m2-2am-2对任意的a∈[-1,1]恒成立,
亦即m2-2am-3≥0对任意的a∈[-1,1]恒成立.
令g(a)=-2ma+m2-3,
只须$\left\{\begin{array}{l}g(-1)={m}^{2}+2m-3≥0\\ g(1)={m}^{2}-2m-3≥0\end{array}\right.$,解得m∈[-1,1]
点评 本题考查的知识点是函数恒成立问题,函数的最值,函数的单调性,难度中档.

练习册系列答案
相关题目
14.若实数x,y满足不等式组$\left\{\begin{array}{l}x+3y-3≥0\\ 2x-y-3≤0\\ x-y+1≥0\end{array}\right.$则z=4x+3y的最大值为( )
| A. | 3 | B. | $\frac{57}{7}$ | C. | 28 | D. | 31 |
11.对于?x∈[${\frac{1}{2}$,+∞)都有2x+a≥$\sqrt{2x-1}$恒成立,则a的取值范围为( )
| A. | $({-∞,-\frac{1}{4}}]$ | B. | $[{-\frac{1}{4},+∞})$ | C. | $({-∞,-\frac{3}{4}}]$ | D. | $[{-\frac{3}{4},+∞})$ |
18.已知集合M={x∈Z|x<3},N={x|1≤ex≤e},则M∩N等于( )
| A. | ∅ | B. | {0} | C. | [0,1] | D. | {0,1} |
8.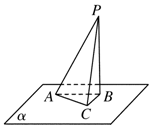 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )| A. | 一条线段 | B. | 一条直线 | ||
| C. | 一个圆 | D. | 一个圆,但要去掉两个点 |
13.已知数列{an}的前n项和为Sn,直线y=x-2$\sqrt{2}$与圆x2+y2=2an+2交于An,Bn(n∈N*)两点,且$S{\;}_n=\frac{1}{4}{|{{A_n}{B_n}}|^2}$.若a1+2a2+3a3+…+nan<λan2+2对任意n∈N*恒成立,则实数λ的取值范围是( )
| A. | (0,+∞) | B. | $(\frac{1}{2},+∞)$ | C. | [0,+∞) | D. | $[\frac{1}{2},+∞)$ |