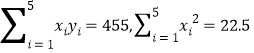题目内容
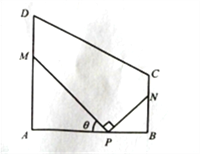
【题目】桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块![]() 平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为
平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为![]() 米,如图,设池塘所占总面积为
米,如图,设池塘所占总面积为![]() 平方米.
平方米.
(Ⅰ)试用![]() 表示
表示![]() .
.
(Ⅱ)当![]() 取何值时,才能使得
取何值时,才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.

【答案】(1)![]()
![]() (2)
(2)![]() 时,
时,![]() 取得最大值
取得最大值![]()
【解析】分析:(1)由已知该项目占地为1800平方米的矩形地块,我们可得![]() ,结合图形及
,结合图形及![]() ,由此我们易将池塘所占面积S表示为变量x的函数;
,由此我们易将池塘所占面积S表示为变量x的函数;
(2)要求S的最大值,根据![]() ,直接使用基本不等式,即可求得最大值.
,直接使用基本不等式,即可求得最大值.
详解:(![]() )由题可得:
)由题可得:![]() ,则
,则![]() ,即
,即![]() .
.
∴![]()
![]()
![]()
![]() .
.
(![]() )∵
)∵![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,取等号,
时,取等号,
∴![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: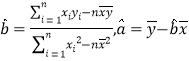
参考数据: