题目内容
设α∈R,函数f(x)=
sin 2xcos α+cos 2xsin α-cos(2x+α)+cos α,x∈R.
(1)若α∈[
,
],求f(x)在区间[0,]上的最大值;
(2)若f(x)=3,求α与x的值.
解:(1)易知f(x)=sin(2x+α)-cos(2x+α)+cos α
=2sin(2x+α-)+cos α,
由于α-∈[0,],
2x+α-∈[α-,α+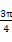
],
所以当2x+α-=,
即x=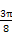
-
时,f(x)max=2+cos α.
又f(x)max=2+cos α在α∈[,]上单调递减,
所以f(x)max=2+cos α≤2+
,
当α=时取到最大值.
综上可知,当α=,x=时,f(x)max=2+.
(2)由于f(x)=2sin(2x+α-)+cos α,
且2sin(2x+α-)≤2,cos α≤1,
现在已知f(x)=3,则等价于
解得
练习册系列答案
名校课堂系列答案
相关题目
=1,则
的值是( )
sin(x+
)
,
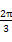]上是增函数
,
]上是减函数
,
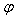)(A>0,ω>0,|
)的部分图象如图所示,则函数y=f(x)对应的解析式为( )
)
),赛道的后一部分为折线段MNP,求A,ω的值和M,P两点间的距离.
),β∈(0,
,则( )
+
=
;
+
=
;
=