题目内容
【题目】设曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,两个焦点分别是是
轴上的椭圆,两个焦点分别是是![]() ,
,![]() ,且
,且![]() ,
,![]() 是曲线上的任意一点,且点
是曲线上的任意一点,且点![]() 到两个焦点距离之和为4.
到两个焦点距离之和为4.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() :
:![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
【答案】(1)![]() (2)证明见解析,直线恒过定点
(2)证明见解析,直线恒过定点![]()
【解析】
(1)根据椭圆的定义得![]() ,又焦点提供出
,又焦点提供出![]() 值,从而可得
值,从而可得![]() ,最终得椭圆方程.
,最终得椭圆方程.
(2)首先明确![]() ,设
,设![]() ,
,![]() ,把直线方程
,把直线方程![]() 代入椭圆方程可得
代入椭圆方程可得![]() ,注意
,注意![]() ,由
,由![]() ,∴
,∴![]() ,即
,即![]() ,代入
,代入![]() 可得
可得![]() 关系(要满足直线与椭圆相交),把这个关系代入直线方程可得出直线所过的定点.
关系(要满足直线与椭圆相交),把这个关系代入直线方程可得出直线所过的定点.
(1)设椭圆方程为![]() ,
,
由题意![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程是
的方程是![]() .
.
(2)由(1)可知![]() ,设
,设![]() ,
,![]() ,
,
联立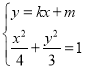 ,得
,得![]() ,
,
![]() ,
,
即![]() ,
,
∴![]() ,
,![]() ,
,
又![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
解得![]() ,
,![]() ,且均满足即
,且均满足即![]() ,
,
当![]() 时,
时,![]() 的方程为
的方程为![]() ,直线恒过
,直线恒过![]() ,与已知矛盾;
,与已知矛盾;
当![]() ,
,![]() 的方程为
的方程为![]() ,直线恒过
,直线恒过![]() .
.

练习册系列答案
相关题目