题目内容
【题目】已知点![]() 在椭圆
在椭圆![]() :
:![]() (
(![]() )上,且点
)上,且点![]() 到左焦点
到左焦点![]() 的距离为3.
的距离为3.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,与直线
为坐标原点,与直线![]() 平行的直线
平行的直线![]() 交椭圆
交椭圆![]() 于不同两点
于不同两点![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)点A在椭圆上则点A的坐标满足椭圆方程,再由![]() 利用两点之间的距离公式列出方程,结合椭圆中a,b,c之间的关系即可求出a,b,c,从而求得椭圆方程;(2)设直线
利用两点之间的距离公式列出方程,结合椭圆中a,b,c之间的关系即可求出a,b,c,从而求得椭圆方程;(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立得关于y的一元二次方程,利用韦达定理求出
,与椭圆方程联立得关于y的一元二次方程,利用韦达定理求出![]() 、
、![]() 关于m的表达式,由弦长公式求出
关于m的表达式,由弦长公式求出![]() 及点
及点![]() 到
到![]() 的距离d,从而求得
的距离d,从而求得![]() 的面积的关于m的表达式,利用基本不等式可求得最大值.
的面积的关于m的表达式,利用基本不等式可求得最大值.
(1)因为椭圆![]() 经过点
经过点![]() ,所以
,所以![]() .
.
设![]() (
(![]() ),则由
),则由![]() 得
得![]() ,解得
,解得![]() .
.
又![]() ,于是
,于是![]() ,解得
,解得![]() (舍负),进而
(舍负),进而![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)因为![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() (
(![]() ),
),
代入![]() 并整理得
并整理得![]() .由
.由![]() 得
得![]() .
.
设![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
所以![]()
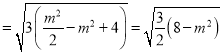 .
.
又点![]() 到
到![]() 的距离
的距离![]() ,所以
,所以![]() 的面积
的面积![]() .
.
故![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目