题目内容
20.已知直角三角形ABC的斜边为AB,且A(-1,0),B(3,0),求:(1)直角顶点C的轨迹方程;
(2)直角边BC的中点M的轨迹方程.
分析 (1)利用直角三角形的性质,圆的定义,即可求出直角顶点C的轨迹方程;
(2)利用代入法,求出直角边BC的中点M的轨迹方程.
解答 解:(1)设AB中点为D,由中点坐标公式得D(1,0),由直角三角形的性质知,|CD|=$\frac{1}{2}$|AB|=2,
由圆的定义知,动点C的轨迹是以D(1,0)为圆心,2为半径长的圆(由于A,B,C三点不共线,所以应除去与x轴的交点).
所以直角顶点C的轨迹方程为(x-1)2+y2=4(x≠3且x≠-1).
(2)设点M(x,y),点C(x0,y0),
因为B(3,0),M是线段BC的中点,由中点坐标公式得x=$\frac{{x}_{0}+3}{2}$(x≠3且x≠1),y=$\frac{{y}_{0}}{2}$,
于是有x0=2x-3,y0=2y.
由(1)知,点C在圆(x-1)2+y2=4(x≠3且x≠-1)上运动,
将x0,y0代入该方程得(2x-4)2+(2y)2=4,即(x-2)2+y2=1.
因此动点M的轨迹方程为(x-2)2+y2=1(x≠3且x≠1).
点评 本题考查圆的方程,考查代入法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.函数$f(x)=\sqrt{\frac{2-x}{x+2}}$的定义域为( )
| A. | (-2,2) | B. | [-2,2] | C. | (-2,2] | D. | [-2,2) |
10.将函数y=sin(2x+φ)(φ>0)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到一个偶函数的图象,则φ的最小值为( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $\frac{3π}{8}$ |
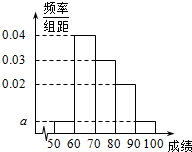 某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].