题目内容
16. 四面体D-ABC中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.
四面体D-ABC中,AB=BC,在侧面DAC中,中线AN⊥中线DM,且DB⊥AN.(1)求证:MN∥面DAB;
(2)平面ACD⊥平面ABC.
分析 (1)连接MN,由已知可得MN∥AD,再由线面平行的判定可得MN∥平面ABD;
(2)AN⊥DM,AN⊥DB,由线面垂直的判定可得AN⊥平面BDM,得到AN⊥BM,在△ABC中,再由已知可得AC⊥BM.由线面垂直的判定可得BM⊥平面ACD,进一步得到平面ACD⊥平面ABC.
解答 证明:(1)连接MN,∵CN=ND,CM=MA,∴MN∥AD,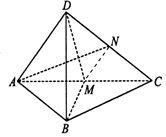
∵MN?平面ABD,AD?平面ABD,∴MN∥平面ABD;
(2)∵AN⊥DM,AN⊥DB,且DB∩DM=D,
∴AN⊥平面BDM,
∵BM?平面BDM,∴AN⊥BM,
又∵△ABC中,AB=BC,且M为AC的中点,∴AC⊥BM.
∵AN,AC时平面ACD内的两条相交直线,
∴BM⊥平面ACD,
∵BM?平面ABC,∴平面ACD⊥平面ABC.
点评 本题考查直线与平面平行,平面与平面垂直的判定,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
7.已知z=1+i,则${z^2}+\overline{z}$=( )
| A. | 1+2i | B. | 1-2i | C. | 1+i | D. | 1-i |
11.抛物线y2=2px的准线经过点(-2,0),则该抛物线的焦点坐标为( )
| A. | (-2,0) | B. | (2,0) | C. | (0,-1) | D. | (0,1) |
1.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| C. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
 已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是3,2.
已知函数f(x)=Asinωx(A>0,ω>0)的图象如图所示,则A,ω的值分别是3,2.