Question

已知向量=a，=b，∠AOB=60°，且|a|=|b|=4.

(1)求|a+b|,|a-b|；

(2)求a+b与a的夹角及a-b与a的夹角.

Answer 1

解法一：

(1)|a+b|²=(a+b)²=a²+2a·b+b²=|a|²+2|a||b|cos60°+|b|²=4²+2×4×4cos60°+4²=16+16+16=48,∴|a+b|=43.

|a-b|²=(a-b)²=a²-2a·b+b²=|a|²-2|a||b|cos60°+|b|²=4²-2×4×4cos60°+4²=16-16+16=16,∴|a-b|=4.

(2)记a+b与a的夹角为α，a-b与a的夹角为β,则

cosα=,∴α=30°.

cosβ=.

∴α=60°.

解法二：如图，以OA,OB为邻边作平行四边形OACB.

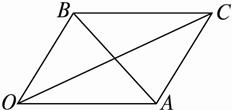
∵|a|=|b|=4，∴四边形OACB为菱形.

(1)a+b=，a-b=，又∠AOB=60°，

∴|a+b|=||=2||=2××4=,a-b=||=4.

(2)在△OAC中，∠OAC=120°，

∴∠COA=∠OCA=30°.a+b与a的夹角即∠COA=30°，a-b与a的夹角即与所成的角为60°.