题目内容
设F1,F2分别是椭圆E: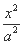 +
+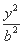 =1(a>b>0)的左、右焦点,过点F1且斜率为1的直线l与椭圆E相交于A,B两点,且AF2,AB,BF2成等差数列.
=1(a>b>0)的左、右焦点,过点F1且斜率为1的直线l与椭圆E相交于A,B两点,且AF2,AB,BF2成等差数列.
(1) 求椭圆E的离心率;
(2) 设点P(0,-1)满足PA=PB,求椭圆E的方程.
(1) 由椭圆定义知AF2+BF2+AB=4a,又由题意知2AB=AF2+BF2,
得AB= a.设l的方程为y=x+c,其中c=
a.设l的方程为y=x+c,其中c= .
.
设A(x1,y1),B(x2,y2),则A,B两点坐标满足方程组
化简得(a2+b2)x2+2a2cx+a2(c2-b2)=0
则x1+x2= ,x1x2=
,x1x2= .
.
因为直线AB斜率为1,所以AB=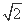 |x2-x1|=
|x2-x1|= ,
,
得 a=
a= ,故a2=2b2,
,故a2=2b2,
所以E的离心率e= =
= =
= .
.
(2) 设AB的中点为N(x0,y0),由(1)知
x0= =
= =-
=- c,y0=x0+c=
c,y0=x0+c= .
.
由PA=PB,得kPN=-1,即 =-1,解得c=3,从而a=3
=-1,解得c=3,从而a=3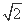 , b=3.
, b=3.
故椭圆E的方程为 +
+ =1.
=1.

练习册系列答案
相关题目
对一位运动员的心脏跳动检测了8次,得到如下表所示的数据:
| 检测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 检测数据ai(次/分钟) | 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
上述数据的统计分析中,一部分计算见如图所示的程序框图(其中 是这8个数据的平均数),则输出的值是 .
是这8个数据的平均数),则输出的值是 .

 的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m= .
的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m= .  -
-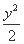 =1的焦距为 .
=1的焦距为 .  },P={y|y=
},P={y|y= },那么M∩P=( )
},那么M∩P=( ) },a=
},a= ,其中b∈(0,1),则下列关系中正确的是( )
,其中b∈(0,1),则下列关系中正确的是( ) ,则f(
,则f( )+f(
)+f( )=( )
)=( ) B.
B. D.-
D.-