题目内容
14.已知函数y=f(x)恒满足f(x+2)=f(x),且当x∈[-1,1]时,f(x)=2|x|-1,则函数g(x)=f(x)-|lgx|在R上的零点的个数是8.分析 作出f(x)与y=|lgx|的函数图象,根据函数图象的交点个数得出答案.
解答 解:∵f(x+2)=f(x),∴f(x)的周期为2,
令g(x)=0得f(x)=|lgx|,
作出y=f(x)与y=|lgx|的函数图象如图所示: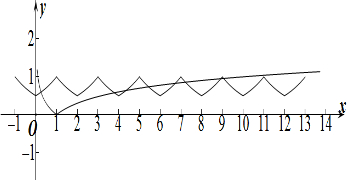
由图象可知f(x)与y=|lgx|在(0,1)上必有1解,
又f(x)的最小值为$\frac{1}{2}$,f(x)的最大值为1,
∵lg2<lg$\sqrt{10}$=$\frac{1}{2}$,lg4>lg$\sqrt{10}$=$\frac{1}{2}$,lg9<1,lg11>1,
∴f(x)与y=|lgx|在(10,+∞)上没有交点,
结合图象可知f(x)与y=|lgx|共有8个交点,
∴g(x)共有8个零点.
故答案为:8.
点评 本题考查了函数零点与图象的关系,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
9.双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)$的离心率为$\sqrt{5}$,则其渐近线方程为( )
| A. | $y=±\frac{1}{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{6}}}{6}x$ | D. | $y=±\sqrt{6}x$ |
6.已知(3-2x)2017=a0+a1(x-1)+a2(x-1)2+…+a2017(x-1)2017,则a1+2a2+3a3+…+2017a2017=( )
| A. | 1 | B. | -1 | C. | 4034 | D. | -4034 |
3.某公司对应聘人员进行能力测试,测试成绩总分为150分.下面是30位应聘人员的测试成绩的测试成绩:64,116,82,93,102,82,104,67,93,118,70,95,119,106,83,72,95,106,72,119,122,95,86,74,131,76,88,108,97,123.
(1)求应聘人员的测试成绩的样本平均数$\overline x$(保留小数点后两位);
(2)根据以上数据完成下面茎叶图:
(3)由茎叶图可以认为,应聘人员的测试成绩Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,其中s2=18.872,利用该正态分布,求P(76.40<Z<114.14).
附:若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,
P(μ-2σ<Z<μ+2σ)=0.9544.
(1)求应聘人员的测试成绩的样本平均数$\overline x$(保留小数点后两位);
(2)根据以上数据完成下面茎叶图:
| 应聘人员的测试成绩 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
附:若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,
P(μ-2σ<Z<μ+2σ)=0.9544.
12.集合﹛x∈Z|(x-2)(x2-3)=0﹜用列举法表示为( )
| A. | ﹛2,$\sqrt{3}$,-$\sqrt{3}$﹜ | B. | ﹛2,$\sqrt{3}$,﹜ | C. | ﹛2,-$\sqrt{3}$﹜ | D. | ﹛2﹜ |
 如图,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为B1C1的中点.