题目内容
2.在数列{an}中,若a1=2,an+1=(-1)n(an-1),则a5=2,前2015项和S2015=1005.分析 通过计算出数列的前几项的值可知该数列为周期数列,进而计算可得结论.
解答 解:∵a1=2,an+1=(-1)n(an-1),
∴a2=-(a1-1)=-1,
a3=a2-1=-2,
a4=-(a3-1)=3,
a5=a4-1=2,
…
由此可知数列{an}是以4为周期的周期数列,
又∵2015=503×4+3,
∴S2015=503×(2-1-2+3)+(2-1-2)=1005,
故答案为:2,1005.
点评 本题考查数列的通项及前n项和,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
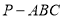 中,
中,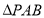 和
和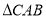 都是以
都是以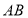 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.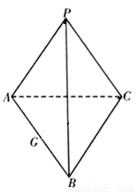
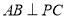 ;
;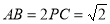 ,求三棱锥
,求三棱锥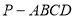 中,
中,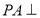 平面
平面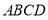 ,底面
,底面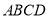 是直角梯形,且
是直角梯形,且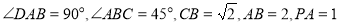 .
.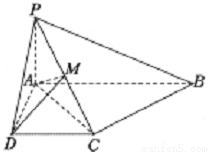
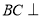 平面
平面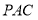 ;
;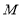 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.