题目内容
已知an=n+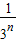
，则数列{an}的前n项和Sn= ．
【答案】分析：根据已知中数列{an}的通项由一个等差数列和一个等比数列相加，可选用拆项法，即分别计算代入公式，求出等差数列和一个等比数列的和，进行解答．
解答：解：∵an=n+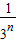
，
∴数列{an}的前n项和Sn=（1+2+…+n）+（
+
+…+
）=
+
=
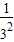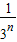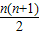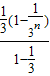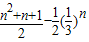
故答案为：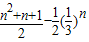
点评：本题考查的知识点是数列求和，其中根据已知数列{an}的通项由一个等差数列和一个等比数列相加，而选择使用拆项法求和，是解答的关键．
解答：解：∵an=n+
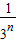，∴数列{an}的前n项和Sn=（1+2+…+n）+（
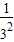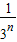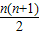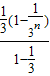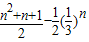
++…+）=+=故答案为：
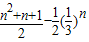
点评：本题考查的知识点是数列求和，其中根据已知数列{an}的通项由一个等差数列和一个等比数列相加，而选择使用拆项法求和，是解答的关键．
练习册系列答案
相关题目
已知an=log（n+1）（n+2），把能够使乘积a1a2a3…an是整数的数字n称为完美数，则在区间（1，2010）内所有的完美数的和为（ ）
| A、1024 | B、2003 | C、2026 | D、2048 |
已知an=2n，把数列{an}各项按如图规律排成三角形数阵，记F（m，n）表示第m行从左至右的第n个数，则F（8，6）=