题目内容
若对任意2≤x≤5,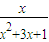 ≤a恒成立,则a的取值范围是 .
≤a恒成立,则a的取值范围是 .
【答案】分析: ≤a恒成立,只要
≤a恒成立,只要 的最大值≤a,故转化为求
的最大值≤a,故转化为求 ,2≤x≤5的最大值问题.
,2≤x≤5的最大值问题.
将分子分母同除以x,分母上函数的单调性求最值即可.
解答:解:因为2≤x≤5,所以令y= ,则y′=1-
,则y′=1- >0,
>0,
所以y= 在[2,5]上单调递增,所以x=2时,y有最小值
在[2,5]上单调递增,所以x=2时,y有最小值
所以有 ,
,
即 的最大值为
的最大值为 ,故
,故 .
.
故答案为:
点评:本题考查不等式恒成立问题、分式不等式求最值、基本不等式求最值的条件等,考查转化思想.
 ≤a恒成立,只要
≤a恒成立,只要 的最大值≤a,故转化为求
的最大值≤a,故转化为求 ,2≤x≤5的最大值问题.
,2≤x≤5的最大值问题.将分子分母同除以x,分母上函数的单调性求最值即可.
解答:解:因为2≤x≤5,所以令y=
 ,则y′=1-
,则y′=1- >0,
>0,所以y=
 在[2,5]上单调递增,所以x=2时,y有最小值
在[2,5]上单调递增,所以x=2时,y有最小值
所以有
 ,
,即
 的最大值为
的最大值为 ,故
,故 .
.故答案为:

点评:本题考查不等式恒成立问题、分式不等式求最值、基本不等式求最值的条件等,考查转化思想.

练习册系列答案
相关题目