题目内容
若对任意2≤x≤5,
≤a恒成立,则a的取值范围是
______.
| x |
| x2+3x+1 |
因为2≤x≤5,所以令y=x+
,则y′=1-
>0,
所以y=x+
在[2,5]上单调递增,所以x=2时,y有最小值
所以有
=
≤
=
,
即
的最大值为
,故a≥
.
故答案为:a≥
| 1 |
| x |
| 1 |
| x2 |
所以y=x+
| 1 |
| x |
| 5 |
| 2 |
所以有
| x |
| x2+3x+1 |
| 1 | ||
x+
|
| 1 | ||
|
| 2 |
| 11 |
即
| x |
| x2+3x+1 |
| 2 |
| 11 |
| 2 |
| 11 |
故答案为:a≥
| 2 |
| 11 |

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
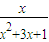 ≤a恒成立,则a的取值范围是 .
≤a恒成立,则a的取值范围是 .