Question

【题目】已知△ABC的边长为2的等边三角形，动点P满足 ，则 的取值范围是 ．

Answer 1

【答案】[﹣ ，0]
【解析】解：如图所示，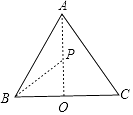
△ABC中，设BC的中点为O，则 =2 ，
∵ = sin2θ +cos2θ =sin2θ +cos2θ
=（1﹣cos2θ） +cos2θ
= +cos2θ（ ﹣ ），
即 ﹣ =cos2θ（ ﹣ ），
可得 =cos2θ ，
又∵cos2θ∈[0，1]，∴P在线段OA上，
由于BC边上的中线OA=2×sin60°= ，
因此（ + ） =2 ，
设| |=t，t∈[0， ]，
可得（ + ） =﹣2t（ ﹣t）=2t2﹣2 t=2（t﹣ ）2﹣ ，
∴当t= 时，（ + ） 取得最小值为﹣ ；
当t=0或 时，（ + ） 取得最大值为0；
∴ 的取值范围是[﹣ ，0]．
所以答案是：[﹣ ，0]．